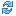Обратная задача имеет одно решение только в том случае, ■если даны cos у, tg у, cotq у или sее у, но если даны sin у и7ii со8< с у, то некоторому sin у или cosec у, в пределах от 0° о 180°, соответствуют дьа угла: у и 180°—у. Для устранения неопределенности необходимо или прямое указание качества угла: остры?! или тупой, или же одновременное задание, кроме sin у или cosec у, еще и другой тригонометрической величины, не являющейся с нею взаимно-обратною величиною: например, неопределенности не будет, если заданы одновременно sin у и cos у, cosec у и tg у и т. д.
Если заданный логарифм тригонометрической величины помечен значком «, то значит тригонометрическая величина отрицательная. В том случае, если значком п обмечен логарифм ■cos у, tq у, cvtg у или sec у, то вычисление ведется как с положительным числом, пммня, однако, что искомый угол ту пий, если же значком п отмечен Log sin у или Loq cosec у, то угла, соответствующего логарифму означенной тригонометрической величины. в пределах от 0° ло 180°, не существует.
В тех случаях, когда логарифмы тригонометрических величин острого угла увеличиваются вместе с увеличением у гла, как это имеет место для Log sin у, Log sec у или Loi tg у, вычисление производится ог ближайшего меньшего логарифма, а когда они уменьшаются вместе с увеличением угла, как у Loq cos у, Log cosec у и Loq coin у,—от ближайшего большего логарифма. В обоих случаях вычисление ведется or ближайшего меньшего угла, и к нему прибавляется поправка за секунды, определяемая по разности между данном и табличным логарифмами и пс табличной разности.
Пример 1 Дан Log sin у = 9,63251, при чем у < 90°; вычислить у. Приискание угла производится следующим образом
Данный Log sin у- 9,63251; 1)=27 Елнжайший меньший табл. Log - 9,6323у для уа 25° 24
ррзность (I = 12 \
для = 9,0 д,^ = 20-
остаток з,о
для 3,2 д^ = 7
искомый угол?/ = 25° 24 27
Поправки на секунды д,(/ и д2?/ вычисляются по вспомогательной табличке с заголовком D = 27; грп этом для приискания десятков секунд берется ближайшее меньшее произведение (в нашем примере 9,0), а для приискания секлнд — вообще ближайшее (в нашем примере 3,2).
Пример 2. Дан тот же Log sin у 9,63251, что и в первом примере, но искомый угол тупой.
Приискание тупого углам може-i быть произведено двояким образом:
lj найти остпый уюл, соответствующий данном} Log sin у = 9,63251; этот угол равен 25"24 27', и затем взять его пополнение до 180°, именно
у- 180° — 25" 24 27"—- 154° 35 33" и 2) пользуясь формулами (lb):
sin у = sin (90" г;) — cos v, мы приискиваем угол г, принимая данный логарифм за Log cos v. и придаем найденное значение г к 90".
Данный Loq sin у = Log cos v = 9,63251 I) 27 Ближайший больший табл. Log. 9,63266 для rt = 64' зС-
разност! (I — 15
для 13,5 1д" V 30
остаток . . 1,5
для . . 1,4, Д2 » = 3
итр-к: v = 64п35'33'

МенюшкаДружественные сайты
|
Убобра.ру - лучший развлекательный портал » Статьи » Решение обратной задачи Решение обратной задачи ↓ |




 Просмотров
Просмотров